Démos
Pathtracing
Cette démo vise à faire du rendu 3D en pathtracing aussi rapidement que possible, en exploitant au maximum le parallelisme et les caches du GPU. Dans un premier temps, la démo vise une certaine simplicité pour mesurer les performances et l'impact des optimisations éventuelles dans un contexte de programmation SIMD.

La scène comporte huit sphères : cinq formant les murs, le sol et le plafond, deux en objets de la scène et une dernière émettant une lumière puissante. Les sphères possèdent toutes le même type de matériau et se différencient par leur couleur de surface, leur rugosité et leur capacité à émettre de la lumière.
Le but du calcul est de simuler avec une relative fidélité le comportement de photon, émis depuis des sources de lumières et s'éparpillant à travers le monde en perdant de l'énergie, ce qui se traduit par un changement de couleur. Relativement simple et basique, cette approche mène naturellement au photoréalisme.
Lancer de rayons
La première étape est de faire fonctionner un lancer de rayon basique, première étape de la simulation de photons. Le but est d'obtenir le rendu suivant :

Un rayon est une demi droite constituée d'un vecteur de direction et d'un point de départ. L'implémentation la plus simple du raytracer consiste à tester la collision avec toutes les sphères et retenir celle ayant entraîné la collision la plus proche.
Approche stochastique et réflections
Dans la réalité, certains objets comme le soleil émettent de la lumière qui va rebondir sur les obstacles qu'elle rencontre en perdant de l'énergie, ce qui se traduit par un changement de couleur.
Il est possible de simuler ce principe dans le programme, en le reproduisant toutefois à l'envers, par des rayons émis depuis le point de vue et se propageant à travers la scène à la recherche de sources de lumière. Pour converger vers un résultat visuel fidèle, le rendu va reposer sur la loi des grands nombres, en utilisant la technique de Monte-Carlo, et en faisant la moyenne de la couleur accumulée par plusieurs photons testés par pixels. Cela donne l'image suivante lorsque les photons rebondissent dans une direction aléatoire sur chaque axe :

Reflection hémisphérique
Les rayons rebondissent en accord avec la rugosité de l'objet atteint. Un objet parfaitement rugueux est supposé renvoyer les rayons reçus dans toutes les directions, mais prendre une valeur de direction au hasard sur chaque axe ne fonctionne pas (aspect "cubique" de l'image du dessus).
La siolution est d'utiliser des coordonnées polaires pour déterminer la nouvelle direction de réflection, qui deviendra hémisphérique :

Cependant, malgré cette amélioration, l'image n'a pas un aspect naturel. Les volumes sont mal soulignés et la répartition de la lumière n'est pas progressive le long de la courbure des objets ronds. Cela provient du fait que la réflection depuis un objet mat n'est pas hémisphérique mais suit une évolution privilégiant un renvoi perpendiculaire à la face, traduit dans le modèle de réflection diffuse.
Reflection diffuse de Lambert
Une adaptation du modèle de réflection en tenant compte dy modèle de Lambert donne le résultat suivant :

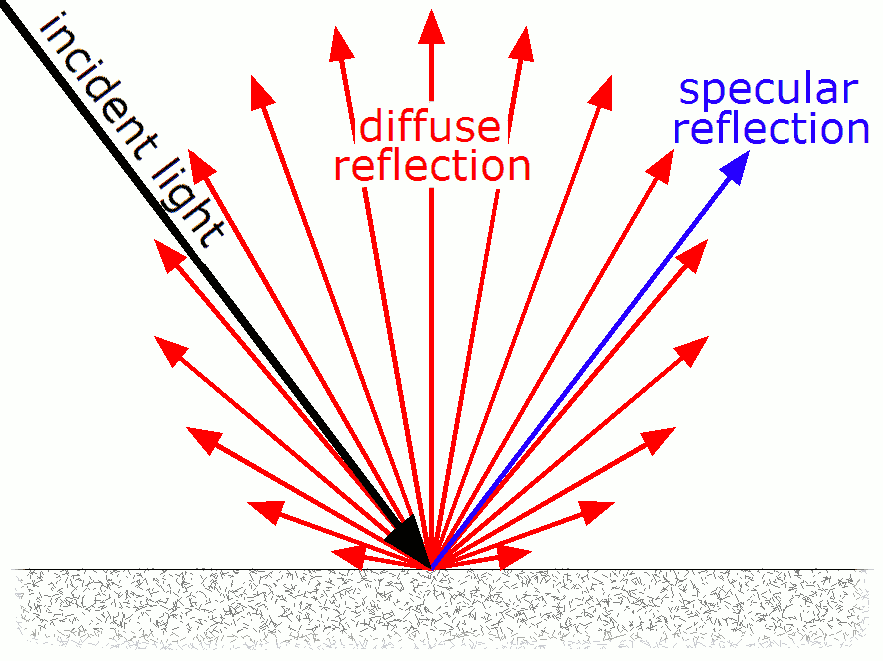
(Image du bas : Wikipedia)
La reflections diffuses est enfin correcte.
Pathtracing et performances
Le vrai défi du rendu 3D est l'éclairage indirect en temps réel. Dans la réalité, la lumière rebondit d'objet en objet en échangeant de l'energie. Pour le simuler dans la démo, il faut extrapoler le principe du raytracing et faire des rayons suivant un chemin de plusieurs rebonds. Pour cela, possibilité d'utiliser de la récursivité ou de manipuler une pile à la main afin de tracer le chemin puis le remonter en sens inverse, en ajoutant/absorbant de l'énergie à chaque obstacle.
Test avec deux rebonds par rayon. L'arrière des objets n'est plus plongé dans le noir absolu :

Test avec cinq rebonds par rayon. On peut voir la couleur des murs déborder sur le sol et le fond, donnant un aspect bien plus chaleureux et crédible à l'image :

Toutes ces démos fonctionnent en temps réel avec des performances raisonnables.
Balls of Steel
Cette particularité du moteur de rendu permet d'envisager un jeu, dont le design serait forcé par l'approche "spécialisée" du pathtracer, ce qui veut dire des graphismes constitués uniquement de sphères, en nombre réduit. Voici Balls of Steel, un brouillon de jeu d'aventure loufoque dans un univers original :


La contrainte principale de conception du jeu est qu'il ne peut y avoir que 64 sphères en tout dans la scène, pouvant chacunes émettre ou réfléchir de la lumière avec une certaine rugosité.
Le rendu est optimisé en privilégiant un nombre de samples élevés vers le milieu de l'écran et plus faible vers les bords de l'écran, ce qui sauve en partie le parallélisme de l'application tout en conservant une qualité visuelle acceptable.
La résolution de l'écran doit être impérativement un multiple de 128 pixels afin de maximiser l'équilibre granularité/monolithisme des blocs CUDA et de ne pas faire un test de sortie de grille. Afin d'augmenter encore plus le framerate, l'image n'est mise à jour qu'une ligne sur trois à chaque frame.
Copyright © Pierre Geissler, 2019 - Tous droits réservés









